week1 - 활성화 함수

활성화 함수

이전 포스팅에서 퍼셉트론의 계산식을 다음과 같이 나타냈습니다.

 

x1*w1+x2*w2+x3*w3 +b <=0 이면 y=0

x1*w1+x2*w2+x3*w3 +b >0 이면 y=1

 

이것을 조금 더 간단히 표현하면,

 

t=x1*w1+x2*w2+x3*w3 +b

y=h(t)

h(x) = 0 (x<=0) , 1 (x>0)

 

즉, t 값이 0이하이면 y는 0이 되고, t 값이 0 초과이면 y는 1이 되는 것 입니다.

 

여기서 h(x)와 같은 함수를 활성화 함수(Activation Function)라고 합니다.

 

 

이해를 위해 여러가지 그림으로 확인하면,

 

활성화함수 그림1

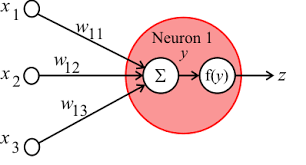
y=x1*w11+x2*w12+x3*w13

f는 activation function

z는 output

 

 

활성화함수 그림2

 

활성화 함수의 종류

 

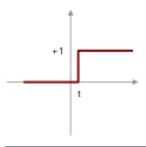
가장 기본이 되는 계단함수

0 또는 1의 값을 출력

 

과거에 많이 사용된 Sigmoid Function

0 ~ 1 사이의 실수값을 출력

(층수가 깊어질수록 Gradient 값이 감소하는 Gradient Vanishing 문제가 있음)

 

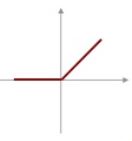
최근 가장 많이 사용되는 ReLU(Rectified Linear Function)

0보다 작거나 같으면 0, 아니면 입력값을 그대로 출력

(Gradient Vanishing 문제를 해결)

 

활성화 함수 코드로 구현하기

 

1. 계단 함수 (Step Function)

def step_function(x):
 
    if x > 0:
        return 1
    else:
        return 0

 

2. 시그모이드 함수 (Sigmoid Function)

import numpy as np
 
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

 

3. ReLU Function

import numpy as np
 
def relu(x):
    return np.maximum(0, x)