신경망 학습
학습이란 훈련 데이터(Train Data)로부터 가중치 매개변수를 갱신하며 최적의 값을 찾는 것 입니다.
이렇게 최적의 값을 찾을 때에 사용하는 하나의 지표가 Loss Function(손실 함수) 입니다.
Loss Function (손실함수)
손실함수는 신경망이 학습할 수 있도록 해주는 지표입니다. 정답과 출력값의 차이, 즉 오차를 말합니다.
이 손실함수 값(=오차)이 최소화되도록 하는 가중치와 편향을 찾습니다 (=학습합니다)
일반적으로는 MSE 혹은 Cross Entropy를 사용합니다.
평균 제곱 오차(Mean Squared Error : MSE)

계산이 간편하여 가장 많이 사용되는 손실 함수입니다. 거리가 음수로 나왔을 때 합산된 오차가 상쇄될 수 있기 때문에 각 거리 차이를 제곱하여 합산한 후에 평균냅니다. 제곱을 하면 거리 차이가 작은 데이터와 큰 데이터 오차의 차이가 더 커지기 때문에 오차가 두드러진다는 장점이 있습니다.
크로스 엔트로피 오차(Cross Entropy Error : CEE)
크로스 엔트로피 오차는 분류(Classification) 문제에서 많이 사용됩니다.

위 식에서 t값이 원-핫 인코딩된 벡터이고, 거기에 모델의 출력 값에 자연로그를 취한 것이 곱해지는 형태입니다. 결과적으로 교차 엔트로피 오차는 정답일 때의 모델 값에 자연로그를 계산하는 식이 됩니다.
예를 들어,
t = [0 0 1], y=[0.1 0.4 0.5] 일 때
t1과 t2는 0이므로 0이되고 결국 t3일 때만 계산이 되어
Error = -ln(0.5)*1 가 나옵니다.
분류 문제에서 모델의 출력은 0에서 1 사이이므로 -log(y)의 함수는 위와 같습니다. 즉, 정답이 1이라고 했을 때, 정답에 근접하는 경우에는 오차가 0에 거의 수렴해갑니다. 그러나 0에 가까워지면, 정답에 멀어지면 멀어질수록 오차가 기하급수적으로 증가하는 것을 볼 수 있습니다. 정답에 멀어질수록 큰 패널티를 부여하는 것입니다.
손실 함수는 매개변수의 변화에 따라 연속적으로 변화합니다. 정확도는 매개변수에 둔감하고, 불연속적으로 변화하기 때문에 미분을 할 수 없습니다. 미분이 되지 않으면 최적화를 할 수 없습니다. 따라서 정확도가 아닌 손실 함수를 지표로 삼아 학습을 해나갑니다.
Gradient Descent Algorithm (경사하강법)

Gradient Descent Algorithm은 어떤 모델에 대한 비용을 최소화 시키는 알고리즘입니다. 머신 러닝 및 딥 러닝 모델에서 사용되는 가중치의 최적 해를 구할때 사용되는 알고리즘입니다. 오차함수의 그레디언트를 사용해 오차 함수의 값이 최소가 되는 위치의 파라미터를 찾는 방법입니다. 오차 함수의 값이 최소인 위치가 어디인지 찾을 때, 임의의 한 점에서 시작하여 오차함수 값이 작아지는 방향으로 조금씩 (Learning Rate에 따라) 이동하면 오차값이 (Local에서 가장) 작은 방향에 도달할 수 있습니다.

이동 속도, 변화율을 조정하는 계수를 Learning Rate (학습률)이라고 합니다. 학습율이 너무 작으면 학습속도가 느리고, 너무 크면 최적값을 찾아가지 못할 수 있습니다.
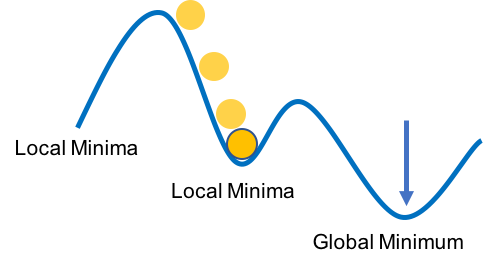
하지만 언덕이나 골짜기가 여러 개인 경우 최적의 해를 보장할 수 없습니다. 지역적으로만 오차가 최소값을 가지는 구간에 갇히게될 수 있는데, 전체 문제에 대한 최적의 solution을 찾을 수 없습니다. 이 구간을 Local minima라고 합니다.
Reference
https://darkpgmr.tistory.com/133
Gradient Descent 탐색 방법
기본적인 함수 최적화(optimization) 방법 중 하나인 gradient descent 방법에 관한 글입니다. Gradient descent 방법은 미분의 개념을 최적화 문제에 적용한 대표적 방법 중 하나로서 함수의 local minimum을 찾..
darkpgmr.tistory.com
'대외활동 > DSC CV Study' 카테고리의 다른 글
| week2 - Optimization 최적화 기법 (0) | 2020.01.13 |
|---|---|
| week2 - Backpropagation 오차역전파법 (0) | 2020.01.13 |
| week1 - Tensorflow로 MNIST 이미지 분류하기 (0) | 2020.01.10 |
| week1 - 활성화 함수 (0) | 2020.01.10 |
| week1 - 퍼셉트론, 인공신경망 (0) | 2020.01.06 |